During an oven refill there was no SFTION beam, so we used the available machine time to accelerate protons between 17:00 and 19:00.
The normal supercycle lacks a high-energy cycle to push the magnets to saturation, as experienced during Parallel MD 2024-11-26, so we add an LHCPILOT cycle, and work on the MD5 cycle, placed directly after the 31 GeV SFTION cycle, and one after an MD1 after the LHCPILOT cycle.
Orbits
We extract orbit data from NXCALS BPMs during MD 2024-11-29, and compute the average beam position for the first turn around the ring.
Here the data is extracted from 16:45 - 17:00 UTC, where we have not yet started trimming on the MD5. We verify that the reference current is the same for all MD5 cycles, and align the measurements with the supercycle configuration (i.e. the first MD5 is the one following the SFTION2).
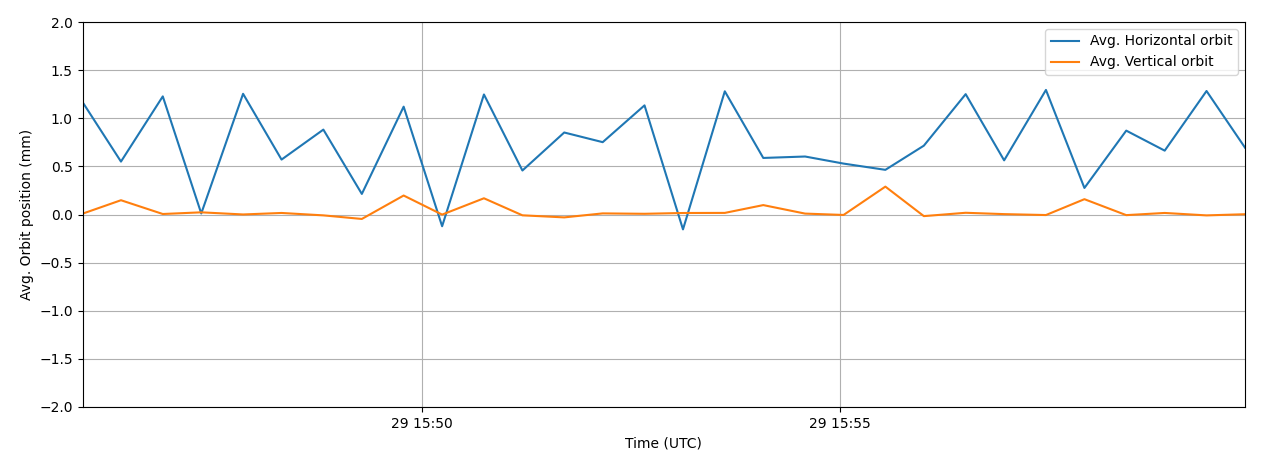Based on the average beam positions (horizontal and vertical), we see significantly higher standard deviation in the horizontal plane than the vertical.
| Mean (mm) | Std (mm) | |
|---|---|---|
| Horizontal | 0.74 | 0.43 |
| Vertical | 0.036 | 0.078 |
To further analyse the beam orbit positions, we plot the individual BPM values along the ring. There are in total 108 BPMs in the SPS.
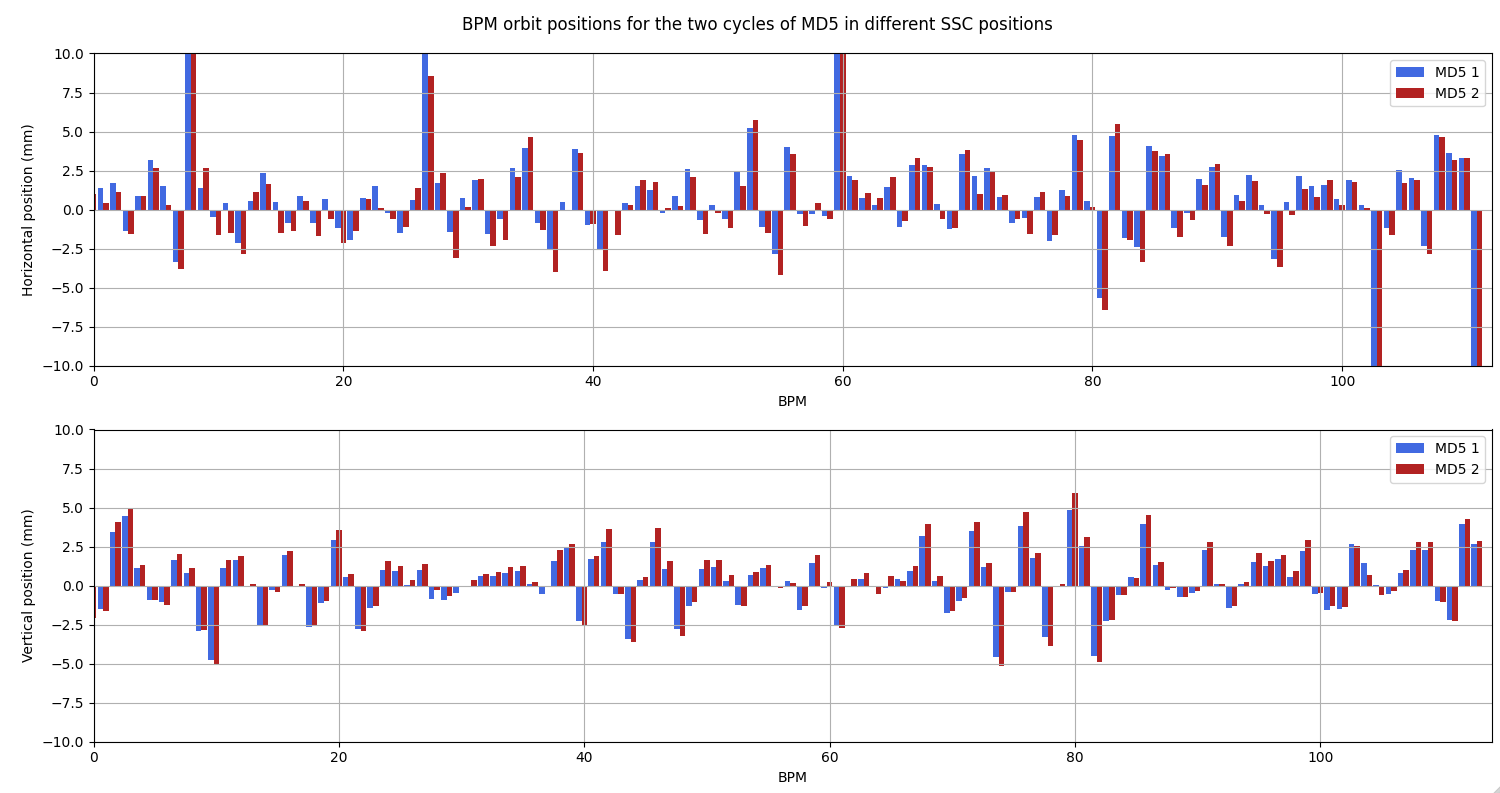
We see that the oscillations are much larger in the horizontal plane than in the vertical plane, and that the peak amplitude of the oscillations are much higher in the horizontal plane.
Trajectories
Extracting the orbits are not sufficient to a comprehensive analysis of the dynamic effects. We instead retrieve the trajectories measured from the BPMs in NXCALS, which are measurements of each individual measured beam path for each turn (whereas orbit is normally averaged over multiple turns).
We can retrieve the trajectories from the first injected turns, and plotting a single BPM (the first BPM after injection in sextant 1) we see:
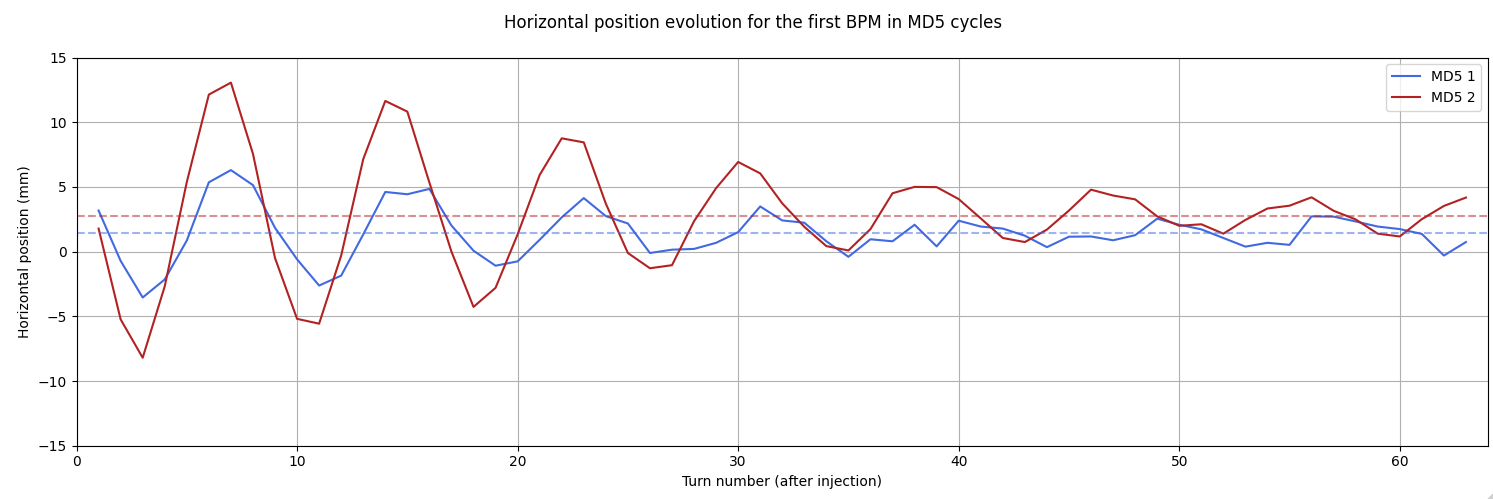
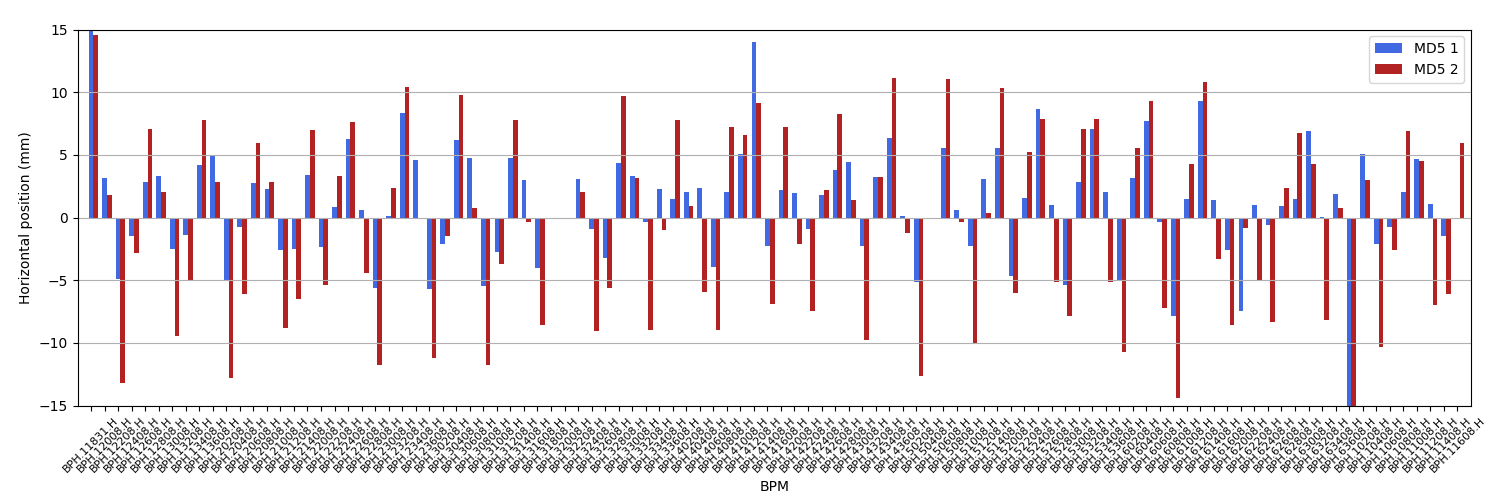
Additionally plotting each individual BPM on the same plot for the first orbit (but note the injection bump on the 0th )
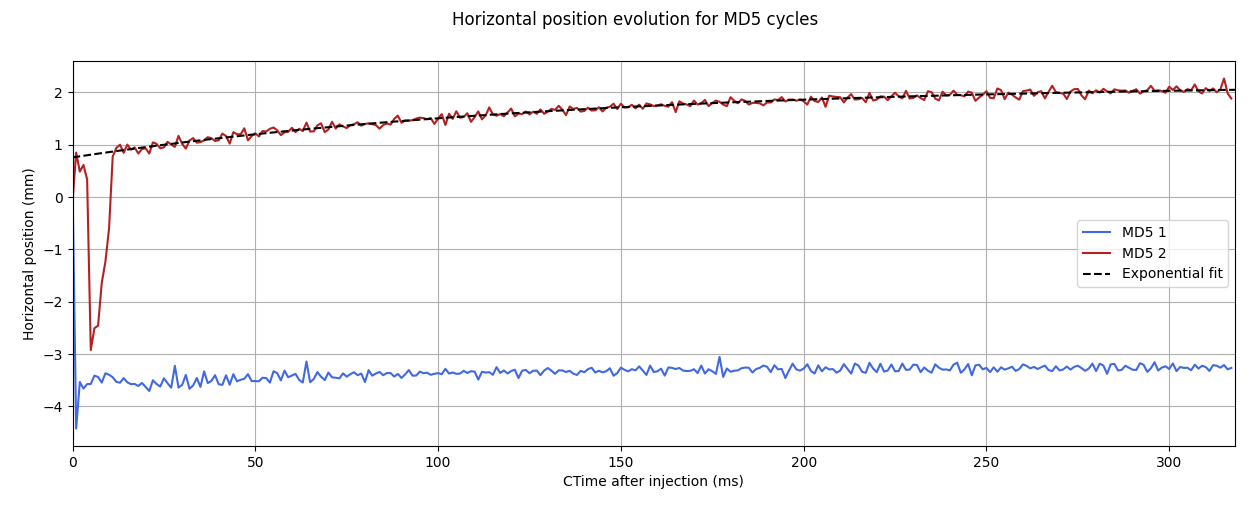
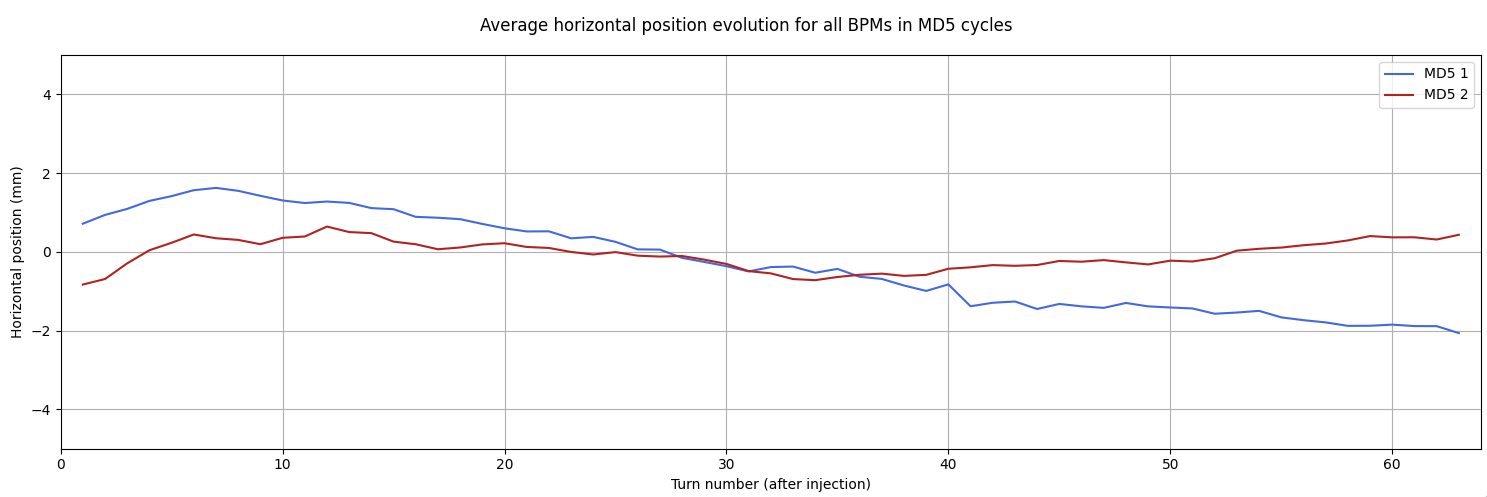
Plotting the average displacement for the first 63 turns we see
Eddy current decay constant
Extracting the positions from all BPMs over time for the 2 MD5 cycles, and fit an exponential to the orbit drift, we see that the movement fits a perfect exponential, with time constant
