Bouc-Wen model for magnetic hysteresis

The equation of motion for sdof systems is expressed as

$$m\ddot{u}(t)+c\dot{u}(t)+F(t)=f(t)$$

where $m$ is the mass, $u(t)$ is the displacement, $c$ the linear viscosity, $F(t)$ the restoring force, and $f(t)$ the excitation force.

According to the Bouc-Wen model, the restoring force is expressed as:

$$F(t)=\underset{elastic}{\underbrace{a{k}_{i}u(t)}}+\underset{hysteretic}{\underbrace{(1-a)k_{f}z(t)}}$$

Where $z(t)$ is a hysteretic variable. So the differential equation can be reformulated to

$$m\ddot{u}(t)+c\dot{u}(t)+a{k}_{i}u(t)+(1-a)k_{f}z(t)=f(t)$$

For magnetic hysteresis, we make the following changes:

$$\{\begin{array}{l}u(t)\to B(t)\\ f(t)\to I(t)\\ z(t)\to r(t)\end{array}$$ $$\ddot{B}(t)+\alpha \dot{B}(t)+a\beta u(t)+(1-a)\gamma r(t)=I(t)$$

Original equation from paper

The original nonlinear equation of motion from the PhyLSTM paper [1] specifies the model as

$$M\ddot{u}+\underset{h}{\underbrace{C\dot{u}+\lambda Ku+(1-\lambda )Kr}}=-M\Gamma a_g$$

Where $M$ is the mass matrices, C the damping matrices, K the stiffness matrices, and u the relative displacement. $\mathbf{r}$ is the hysteretic parameter, $a_g$ represents the ground acceleration, $\lambda$ the ratio of post- and pre-yield stiffness. $\Gamma$ is the force distribution vector, and $h$ represents the total nonlinear restoring force. The equation maps the ground motion $a_g$ to structural response $\mathbf{u},\dot{\mathbf{u}},\ddot{\mathbf{u}}$ and $\mathbf{r}$. Normalizing the equation based on $M$, the equation can be rewritten in a more general form

$$\ddot{\mathbf{u}}+\mathbf{g}=-\mathbf{\Gamma }{a}_g$$

with $\mathbf{g}(t)={\mathbf{M}}^{-1}\mathbf{h}(t)$, and $\mathbf{g}(t)=\mathcal{G}(\mathbf{Z}(\mathbf{t}))$, with $\mathbf{Z}$ being a state space variable.

For dynamic systems with complex rate-dependent hysteretic behavior (dependent on $\dot{\mathbf{r}}$), the equation can be augmented by another nonlinear differential equation:

$$\begin{array}{rl}\ddot{\mathbf{u}}+\mathbf{g}& =-\mathbf{\Gamma }{a}_g\\ \dot{\mathbf{r}}& =f(\mathbf{\Phi })\end{array}$$

For the Bouc-Wen model $\mathbf{\Phi }=\{\Delta \dot{\mathbf{u}},|\Delta \dot{\mathbf{u}}|,\mathbf{r},{\mathbf{r}}^{n-1},{\mathbf{r}}^n\}$, or for a simplified version, $\mathbf{\Phi }=\{\Delta \dot{\mathbf{u}},\mathbf{r}\}$.

Equation adapted for magnetic hysteresis

We adapt the equation above to:

$$\begin{array}{rl}\ddot{\mathbf{B}}+\mathbf{g}& =-\mathbf{\Gamma }I\\ \dot{\mathbf{r}}& =f(\mathbf{\Phi }),\Phi =\{\Delta \dot{\mathbf{B}},\mathbf{r}\}\\ \mathbf{g}& =\mathcal{G}(\mathbf{z}),\mathbf{z}=\{\mathbf{B},\dot{\mathbf{B}},\mathbf{r}\}\end{array}$$

Therefore we are optimizing the above functions so that:

$$\{\begin{array}{ll}{z}_1-B& \to 0\\ z_2-\dot{B}& \to 0\\ {\dot{z}}_1-z_2& \to 0\\ {\dot{z}}_2-(-\Gamma I-g)={\dot{z}}_2+\Gamma I+g& \to 0\\ \dot{r}-{\dot{z}}_3& \to 0\end{array}$$

Where

$$\{\begin{array}{ll}\mathbf{z}& =\{z_1,z_2,z_3\}=\{\hat{B},\hat{\dot{B}},\hat{r}\}={\text{PhyLSTM}}_1(I)\\ \mathbf{\Gamma }I+\mathbf{g}& ={\text{PhyLSTM}}_2(I)\\ \dot{\mathbf{r}}& ={\text{PhyLSTM}}_3(I)\end{array}$$

To investigate

• Self-Adaptive PINN (meta learning of loss weights) for BWLSTM [priority:: low] [completion:: 2024-08-06]

[1]: https://arxiv.org/abs/2002.10253

Implemented in 118b8d86440a8863b40fa61d92a42d5d15662be3.

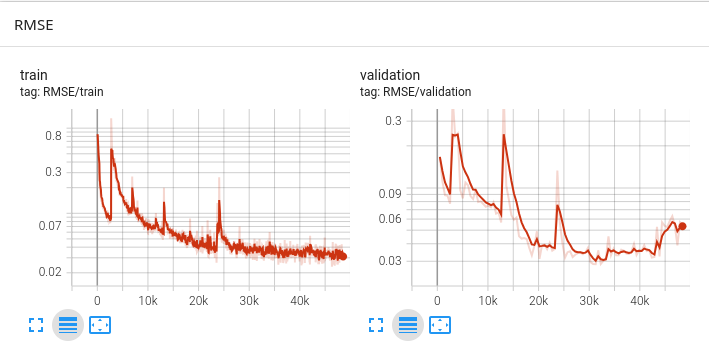
The SA-PINN is trained on 1h of funky MBI data, and evaluated on the SFTPRO+LHC+ZERO dataset.

The loss itself does not converge easily, certainly due to the loss weights increasing over time. To be discovered how initialization of loss weights influence the loss landscape.

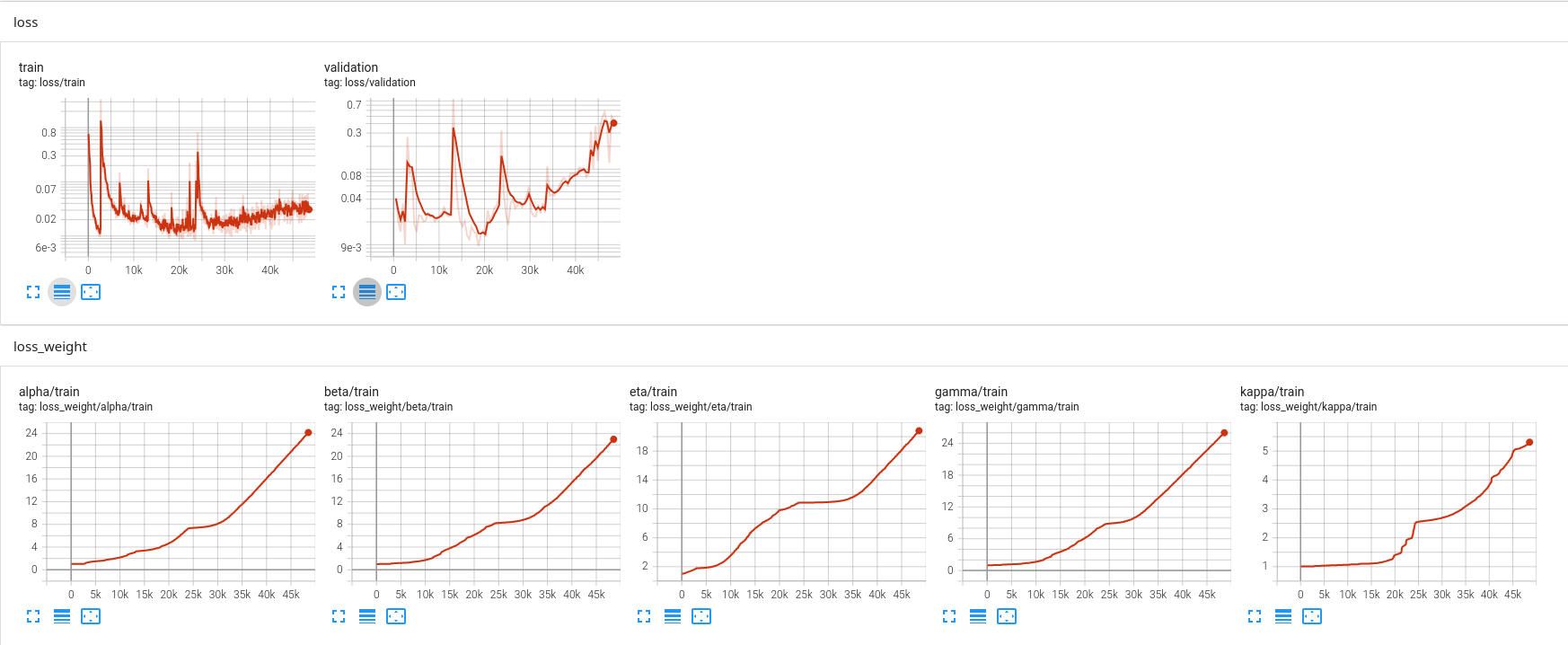
It should be noted however that the RMSE loss is monotonically decreasing, showing that the optimization does in fact work.