Introduction
A significant issue with measured B-train data is the (integration) drift of the field measurements on flat bottom, where even though the measured (and therefore played current) is flat, or decreasing, the measured field is increasing.
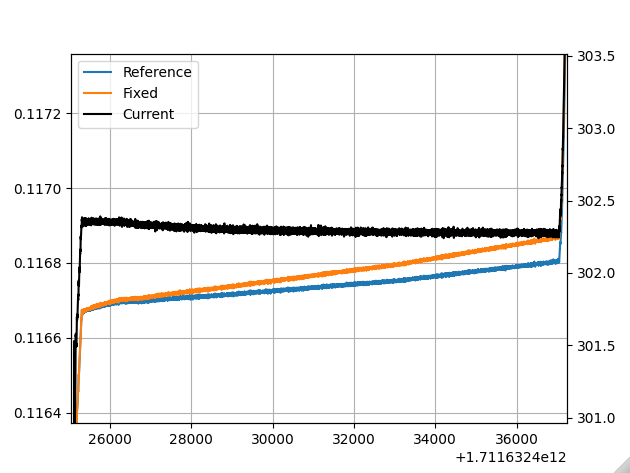If we assume that the drift is linear in short time frames (seconds), and we know when the absolute field is known (i.e. when the marker is applied), we can estimate the drift as the gap between before the marker was applied and after, and subtracting the field difference caused by current changes since the marker is usually applied where the current is ramping.
Calculating the marker index
def marker_idx(i_meas: np.ndarray, b_meas: np.ndarray, marker_value: float = 0.11) -> int:
b_ref = np.interp(i_meas, *calibration_fn.T)
diff = np.gradient(b_meas) - np.gradient(b_ref)
idx = int(np.where(b_meas > marker_value)[0][0])
amin = np.argmin(diff)
amax = np.argmax(diff)
# depending on if the marker direction was up or down
if np.abs(amax - idx) <= 1:
pass
elif np.abs(amin - idx) <= 1:
idx += 1
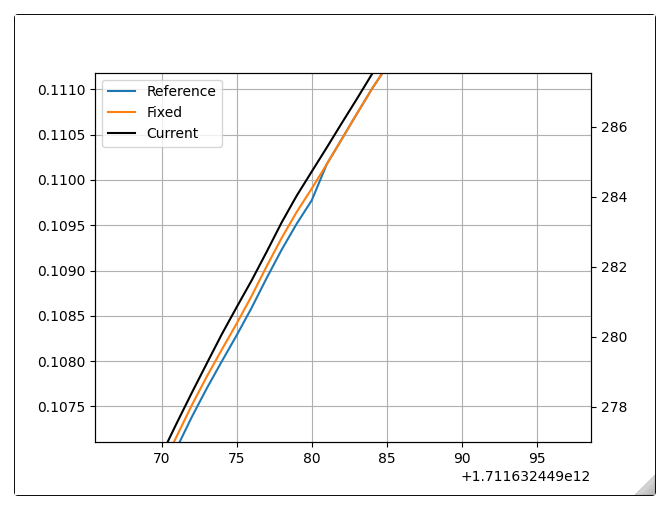
return idxThe index where the marker was applied is computed by finding where the measured field is passing the marker value (since the field is so far always increasing when the marker is applied).
To determine if the marker value decreases or increases the field (positive or negative gap), we take the difference between gradients of the reference field (as computed from measured or reference current, and the Calibration function), and find the highest peak. If the marker gap is negative, we assume the marker was applied at the next index.
Info
Note that the B-train is sampling at a higher frequency at 1 kHz, and then downsampled to 1 kHz. So the marker is applied at a much higher frequency sampling.
Drift-correcting a full dataset
Implementing the drift-correction uses the hysteresis-scripts BTrainDataset convenience class, which allows easily splitting a dataset into individual cycles, making the drift-correction easier to do cycle-by-cycle.
In addition to the dataset, we need the Calibration function to calculate expected (continuous) field from current, in order to calculate the field change when the marker is applied.
def drift_correct(dataset: BTrainDataset, calibration_fn: np.ndarray, *, fix_only: typing.Callable[[str], bool] | str = "") -> BTrainDataset:
dataset = BTrainDataset(dataset.df.copy())
cycles = dataset.aslist()
slices = list(dataset._slices.values()) # noqa: SLF001
for i, (cycle, s) in enumerate(zip(cycles, slices)):
if i == 0:
continue
if callable(fix_only):
if not fix_only(cycle.user):
continue
elif fix_only and cycle.user != fix_only:
continue
idx = marker_idx(cycle.i_meas, cycle.b_meas)
# estimate the field change due to current change
iref = cycle.df["I_ref_A"].to_numpy()
b0 = np.interp(iref[idx-1], *calibration_fn.T)
b1 = np.interp(iref[idx], *calibration_fn.T)
db = b1 - b0
# drift is computed as the gap between the marker and the previous value, minus the field change due to current change
drift = cycle.b_meas[idx] - cycle.b_meas[idx - 1]
drift -= db
# retrieve the previous cycle so we know how long the drift correction should be
prev_cycle = cycles[i - 1]
idx_prev = marker_idx(prev_cycle.i_meas, prev_cycle.b_meas)
dt = len(prev_cycle.i_meas) - idx_prev + idx
# fix the previous cycle
b_meas_prev = prev_cycle.df["B_meas_T"].to_numpy()
corr = drift * np.arange(len(b_meas_prev) - idx_prev) / dt
b_meas_prev[idx_prev:] += corr
dataset.df["B_meas_T"].iloc[slices[i - 1]] = b_meas_prev
# fix the current cycle
b_meas_corrected = cycle.df["B_meas_T"].to_numpy()
corr = drift * np.arange(len(prev_cycle.i_meas) - idx_prev + 1, dt + 1) / dt
b_meas_corrected[:idx] += corr
dataset.df["B_meas_T"].iloc[s] = b_meas_corrected
return dataseResults
We attempt the drift-correction on an LHC-type cycle followed by an MD1. The gap is smoothed out (not perfectly, but sufficiently), by shifting the field between the marker of the LHC25NS and MD1 by around 1-2 Gauss. However while this reduces the drift of the MD1, the drift on the LHC25NS is worsened as seen in Introduction.
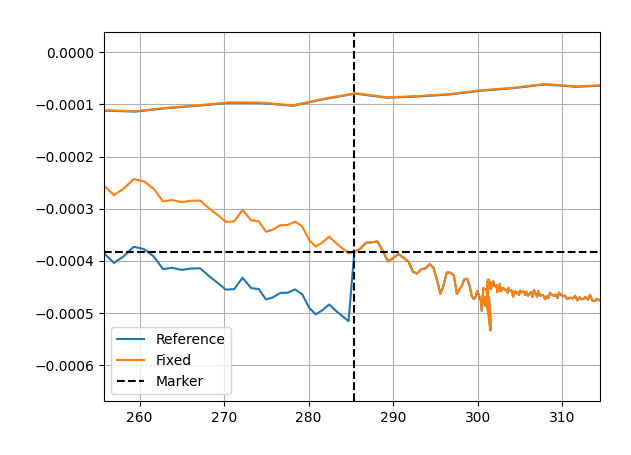As we see on the phase-space of the MD1, we see that the marker is gap is fixes almost perfectly, but worsens the LHC cycle.
Marking only SFT-type cycles
Since in all operational cases, an SFT-type cycle is always preeceeded with an MD1, and we don’t significantly care about the hysteresis on the MD1 cycle, we can drift-correct on the SFT-type cycle to improve the field measurements on the flat bottom.
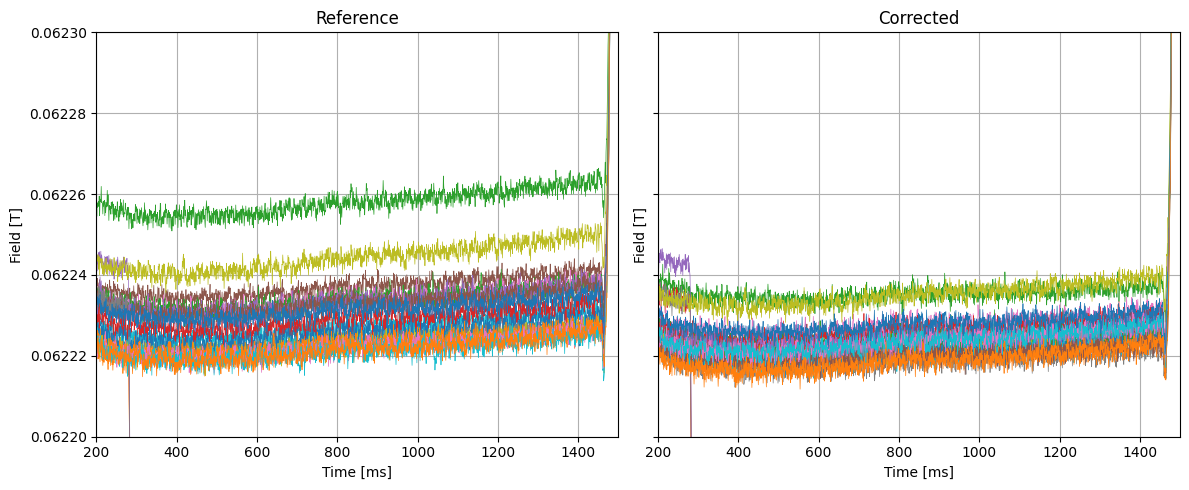
We see that applying drift correction on the SFT cycle (where the marker is applied immediately after the injection plateau), we see a significant improvement in the measurements where the “groupings” are tighter, and the green and yellow measurements are “grouped” together. While it is difficult to determine the absolute improvement in measured field since ground truth is missing, we can still make measurements more consistent at the SFT flat bottom, while not touching the flat top.
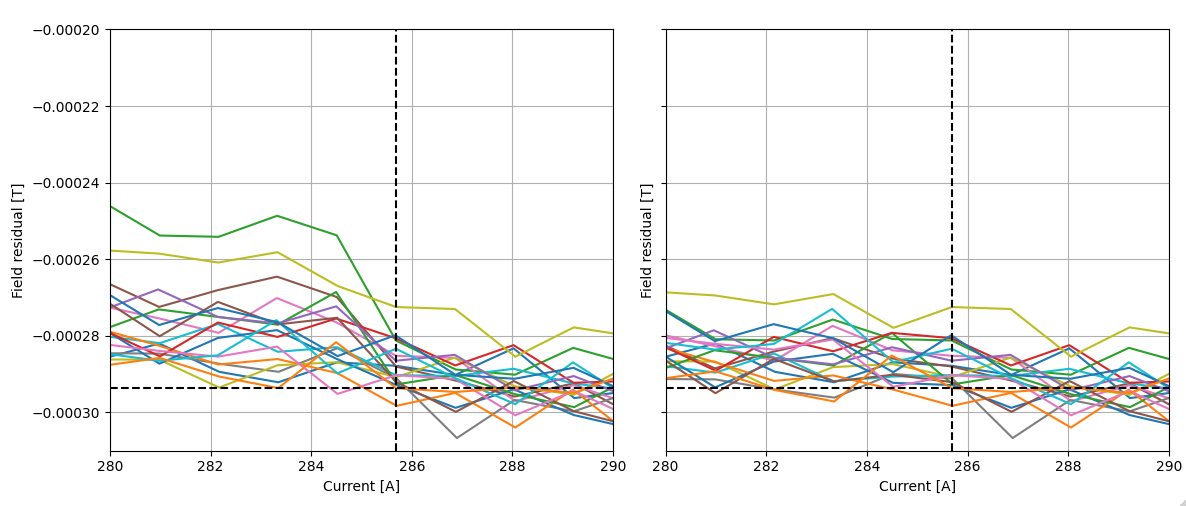We see on the phase-space (here zoomed in on where the marker is applied) that the jump on the green line is improved, however we are reaching the limits of the noise floor for current and field measurements to significantly improve the drift-correction beyond range.
- Drift-correct SFTPRO1 data in Dipole datasets v4 [due:: 2025-03-14] [completion:: 2025-04-14]
Marking on cycles when preceeding cycle is not marked
An improvement to the previous script is needed when the preceeding cycle is not marked, for example when the previous cycle is one or many ZERO cycles.
We improve the script to the following
from __future__ import annotations
import argparse
import os
import pathlib
import shutil
import typing
import sys
import matplotlib.figure
import numpy as np
import pandas as pd
import warnings
import matplotlib.pyplot as plt
from hysteresis_scripts.data import BTrainDataset, BTrainCycle
CALIBRATION_FN_PATH = pathlib.Path(
"~/cernbox/hysteresis/calibration_fn/SPS_MB_I2B_CALIBRATION_FN_v7.csv"
).expanduser()
calibration_fn = np.loadtxt(CALIBRATION_FN_PATH, delimiter=",", skiprows=1)
def marker_idx(
i_meas: np.ndarray, b_meas: np.ndarray, marker_value: float = 0.11
) -> int:
b_ref = np.interp(i_meas, *calibration_fn.T)
diff = np.gradient(b_meas) - np.gradient(b_ref)
idx = int(np.where(b_meas > marker_value)[0][0])
amin = np.argmin(diff)
amax = np.argmax(diff)
# depending on if the marker direction was up or down
if np.abs(amax - idx) <= 1:
pass
elif np.abs(amin - idx) <= 1:
idx += 1
return idx
def marker_applied(i_meas: np.ndarray) -> bool:
"""
Check if the marker was applied in the cycle
"""
return np.mean(i_meas) > 500
def drift_correct(
dataset: BTrainDataset,
calibration_fn: np.ndarray,
*,
fix_only: typing.Callable[[BTrainCycle], bool] | str = "",
) -> BTrainDataset:
dataset = BTrainDataset(dataset.df.copy())
if int(pd.__version__.split(".")[0]) > 2:
msg = "This function is only supported for pandas <3.0.0 due to chained assignment issues"
raise NotImplementedError(msg)
cycles = dataset.aslist()
slices = list(dataset._slices.values()) # noqa: SLF001
last_marker_idx = None
for i, (cycle, s) in enumerate(zip(cycles, slices)):
if last_marker_idx is None:
last_marker_idx = i
continue
fix = True
if callable(fix_only):
if not fix_only(cycle):
fix = False
elif fix_only and cycle.user != fix_only:
fix = False
if not fix:
if marker_applied(cycle.i_meas):
last_marker_idx = i
continue
try:
idx = marker_idx(cycle.i_meas, cycle.b_meas)
idx_candidates = [
idx - 1,
idx,
idx + 1,
]
except IndexError:
continue
best_idx = None
max_drift = 0
for idx in idx_candidates:
if idx < 1 or idx >= len(cycle.b_meas):
continue
# estimate the field change due to current change
iref = cycle.df["I_ref_A"].to_numpy()
b0 = np.interp(iref[idx - 1], *calibration_fn.T)
b1 = np.interp(iref[idx], *calibration_fn.T)
db = b1 - b0
# compute drift
drift = cycle.b_meas[idx] - cycle.b_meas[idx - 1] - db
if np.abs(drift) > max_drift and np.abs(drift) > 1e-5:
max_drift = np.abs(drift)
best_idx = idx
if best_idx is None:
continue
idx = best_idx
# estimate the field change due to current change
iref = cycle.df["I_ref_A"].to_numpy()
b0 = np.interp(iref[idx - 1], *calibration_fn.T)
b1 = np.interp(iref[idx], *calibration_fn.T)
db = b1 - b0
# drift is computed as the gap between the marker and the previous value, minus the field change due to current change
drift = cycle.b_meas[idx] - cycle.b_meas[idx - 1]
drift -= db
if np.abs(drift) < 1e-5:
continue
# retrieve the last cycle where the marker was applied
prev_cycle = cycles[last_marker_idx]
try:
idx_prev = marker_idx(prev_cycle.i_meas, prev_cycle.b_meas)
except IndexError:
continue
# Calculate dt as the total number of points between the previous marker and the current marker, across all cycles in between
dt = 0
for j in range(last_marker_idx, i + 1):
current_cycle = cycles[j]
if j == last_marker_idx:
dt += len(current_cycle.i_meas) - idx_prev
# pass # skip the first cycle
elif j == i:
dt += idx
else:
dt += len(current_cycle.i_meas)
# apply drift correction across all cycles in between
offset = 0
for j in range(last_marker_idx, i + 1):
current_cycle = cycles[j]
current_slice = slices[j]
b_meas = current_cycle.df["B_meas_T"].to_numpy()
i_meas = current_cycle.df["I_meas_A"].to_numpy()
if j == last_marker_idx:
n = len(b_meas) - idx_prev
offset += n
continue
corr = drift * np.arange(offset, offset + n) / dt
b_meas[idx_prev:] += corr
elif j == i:
n = idx
corr = drift * np.arange(offset, offset + n) / dt
b_meas[:idx] += corr
offset += n
else:
n = len(b_meas)
# if not marker_applied(current_cycle.i_meas):
mask = i_meas < 400
corr = drift * np.arange(offset, offset + n) / dt
b_meas[mask] += corr[mask]
offset += n
with warnings.catch_warnings():
warnings.simplefilter("ignore")
dataset.df["B_meas_T"].iloc[current_slice] = b_meas
print(
f"Drift-corrected cycle {cycles[j - 1].user} to {current_cycle.user} dB = {drift * 1e4:.2f} G"
)
last_marker_idx = i
return dataset
def parse_args(argv: list[str]) -> argparse.Namespace:
parser = argparse.ArgumentParser()
parser.add_argument("datasets", type=pathlib.Path, nargs="+")
return parser.parse_args(argv)
def plot_phase_space(
dataset: BTrainDataset, dataset_ref: BTrainDataset
) -> matplotlib.figure.Figure:
fig, ax = plt.subplots()
cycles = dataset.aslist()
cycles = [cycle for cycle in cycles if cycle.cycle.startswith("SFT")]
cycles_ref = [
cycle for cycle in dataset_ref.aslist() if cycle.cycle.startswith("SFT")
]
if len(cycles) != len(cycles_ref):
raise ValueError("Different number of cycles in datasets")
if len(cycles) == 0:
print("No SFT cycles found in dataset")
return fig
for IDX in range(len(cycles)):
cycle = cycles[IDX]
idx = marker_idx(cycle.i_meas, cycles_ref[IDX].b_meas)
ax.plot(
cycle.i_meas,
cycles_ref[IDX].b_meas
- np.interp(cycle.i_meas, calibration_fn[:, 0], calibration_fn[:, 1]),
label="Reference",
color="gray",
linewidth=0.5,
)
ax.plot(
cycle.i_meas,
cycle.b_meas
- np.interp(cycle.i_meas, calibration_fn[:, 0], calibration_fn[:, 1]),
label="Fixed",
color="firebrick",
linestyle="--",
linewidth=0.5,
)
ax.axvline(cycle.i_meas[idx], c="black", linestyle="--", label="Marker")
ax.axhline(
(
cycle.b_meas
- np.interp(cycle.i_meas, calibration_fn[:, 0], calibration_fn[:, 1])
)[idx],
c="black",
linestyle="--",
)
# ax.legend()
ax.grid()
return fig
def drift_correct_dataset(path: pathlib.Path) -> None:
print(f"Drift correcting dataset {path}")
ref_dataset = BTrainDataset.from_parquet(path)
dataset = drift_correct(
BTrainDataset(ref_dataset.df.copy()),
calibration_fn,
fix_only=lambda cycle: cycle.cycle.startswith("SFT"),
# prev_cycle_constr=lambda cycle: cycle.user == "MD1"
# and cycle.df.I_meas_A.max() > 500,
)
if dataset.df.equals(ref_dataset.df):
print(f"No drift correction needed for {path.name}")
return
fig = plot_phase_space(dataset, ref_dataset)
fig.suptitle(f"Drift correction for {path.name}")
plt.show()
# ask user if they want to save the corrected dataset
if input("Save corrected dataset? [y/n] ").lower() == "y":
dataset.to_parquet(path)
def main(argv: list[str]) -> None:
args = parse_args(argv)
datasets = (
[args.datasets] if isinstance(args.datasets, pathlib.Path) else args.datasets
)
datasets = [dataset for dataset in datasets if dataset.exists()]
for dataset_path in datasets:
if (
dataset_path.suffix == ".parquet"
and "preprocessed" not in dataset_path.name
):
drift_correct_dataset(dataset_path)
continue
elif dataset_path.is_dir():
for path in dataset_path.rglob("*"):
if path.suffix == ".parquet" and "preprocessed" not in path.name:
drift_correct_dataset(path)
continue
if __name__ == "__main__":
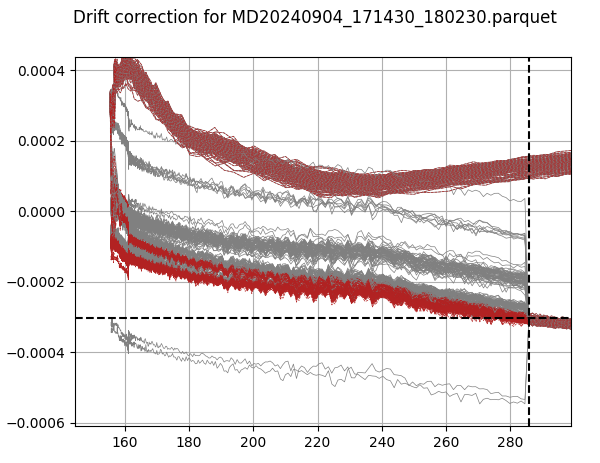
main(sys.argv[1:])By applying the drift-correction on the dataset from Dedicated MD 2024-09-04, we see that the drift-correction is significantly improved, and the data is much more consistent.
By further increasing the guessing-range for marking indices, we can drift-correct even when the marker is not applied exactly at 1100 G (at 1 kHz). We improve over the previous plot to the following:
We see a significant drift correction from Gauss to consistent injection fields for SFTPRO1.
Warning
The drift-correction method explicitly does not mark the first cycle (where the marker was previously applied), to not introduce more errors. The method drift-corrects only cycles that are not marked (ZEROs, flat fields, etc.).
Online drift-correction
Since 2025-08-09 an UCAP converter is deployed for drift-correcting B-Train data using the method above. To validate it, we acquire measurements from the UCAP and the B-Train and plot both to compare:
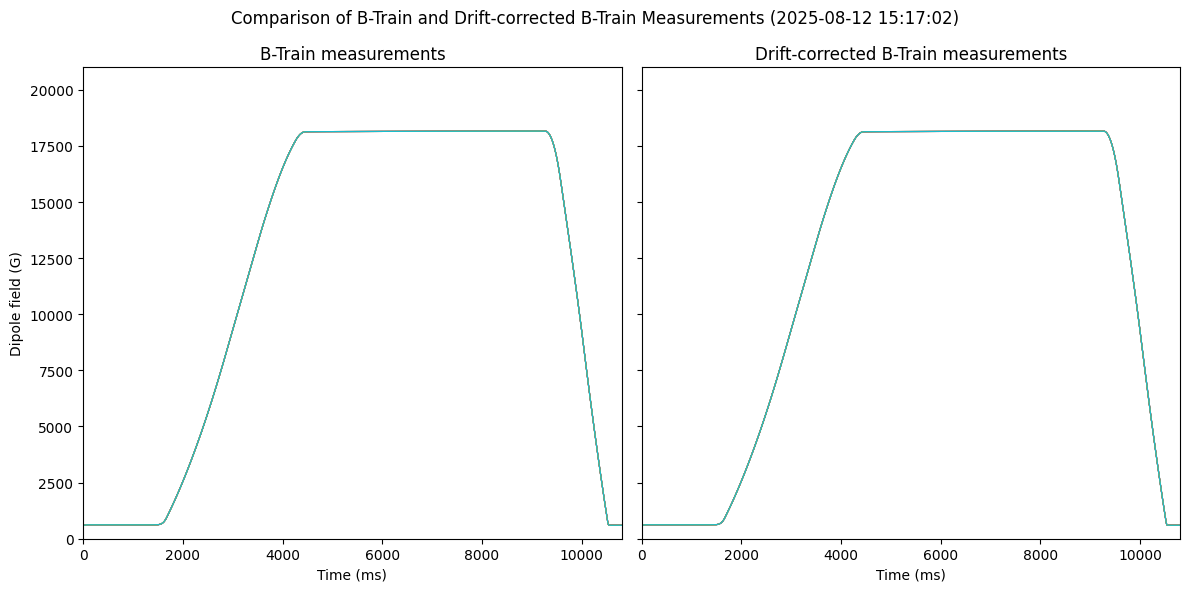
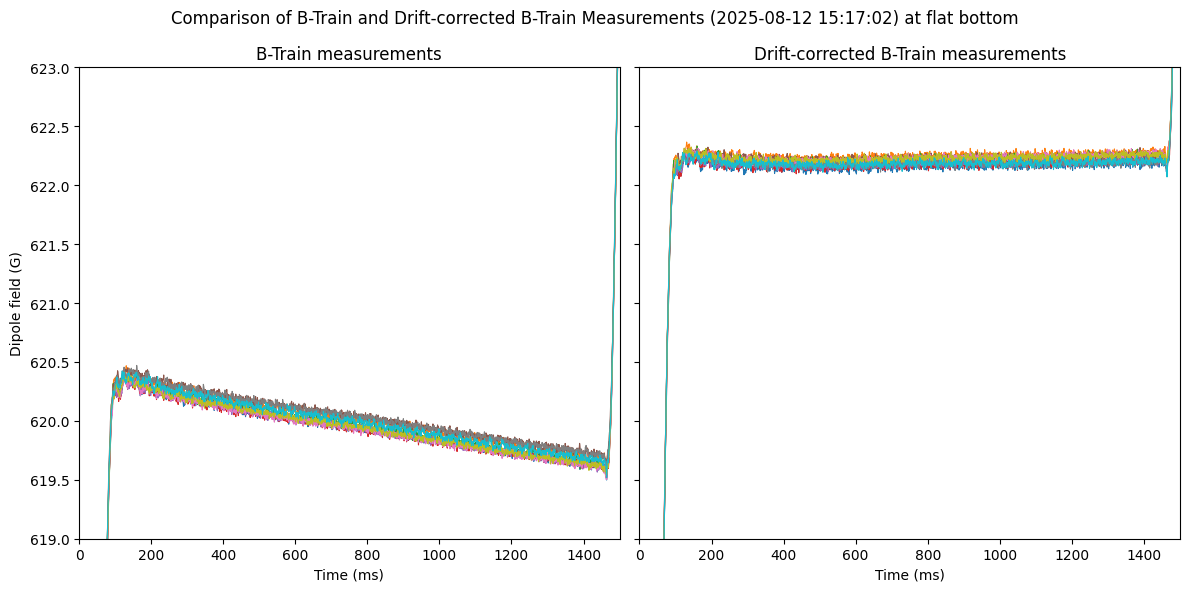
On this day 2025-08-12, the drift is particularly bad and it seems as if the SFT injection plateau is “ramping down”, but when drift-corrected it seems that the injection plateau is actually flat. However compared to the reference field in LSA, which is set to 629.999 G, the drift-corrected measurements are still wrong by 7 G.
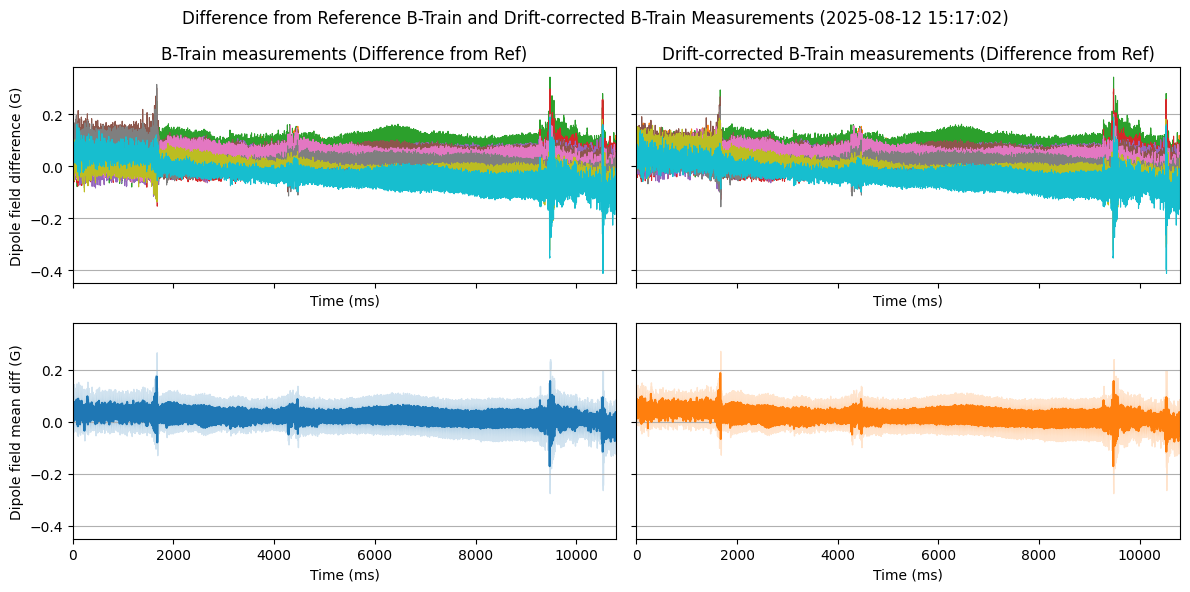
Subtracting every measurement with a reference (first measurement) we see similar std and mean between both measurements