Fit piecewise-linear fn to I-B v5

The piecewise linear function from Fit piecewise-linear fn to I-B v4 shows artifacts on low and high currents. At low fields it is not a good fit due field measurement uncertainties from drift.

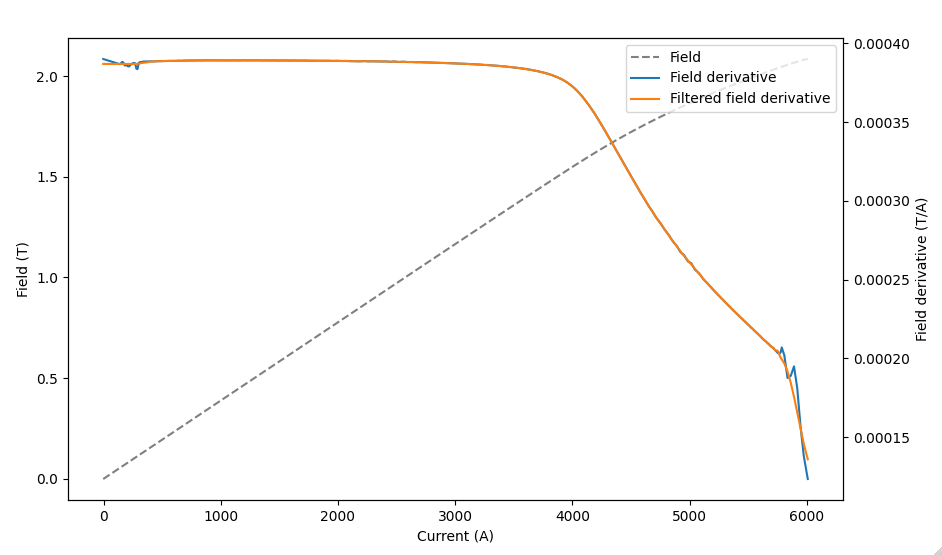
We smooth the calibration function first using a wiki:Savitzky–Golay filter, and then smooth out the edge points by extrapolation using an univariate spline

discrete_fn_v5 = DiscreteFunctionTransform(discrete_fn.xs.copy(), discrete_fn.ys.copy())  
  
lower_thres = 400  # A  
upper_thres = 5700  # A  
  
ys_v5 = discrete_fn_v5.ys  
ys_v5 = scipy.signal.savgol_filter(ys_v5, 11, 1)  
  
weights = np.ones_like(discrete_fn_v5.xs)  
weights[discrete_fn_v5.xs < lower_thres] = 0.1  
weights[discrete_fn_v5.xs >= upper_thres] = 0.01  
weights[-3:] = 2.  
  
points = (discrete_fn_v5.xs >= lower_thres) & (discrete_fn_v5.xs < upper_thres)  
points[-3:] = True  
weights = weights[points]  
  
spline = scipy.interpolate.InterpolatedUnivariateSpline(  
    discrete_fn_v5.xs[points],  
    ys_v5[points],  
    # bbox=[lower_thres, upper_thres],  
    w=weights,  
    k=3,  
    ext=0,  
    # s=.5  
)  
  
# discrete_fn_v5.ys = spline(discrete_fn_v5.xs)  
discrete_fn_v5.ys = ys_v5  
discrete_fn_v5.ys[discrete_fn_v5.xs < lower_thres] = spline(discrete_fn_v5.xs[discrete_fn_v5.xs < lower_thres])  
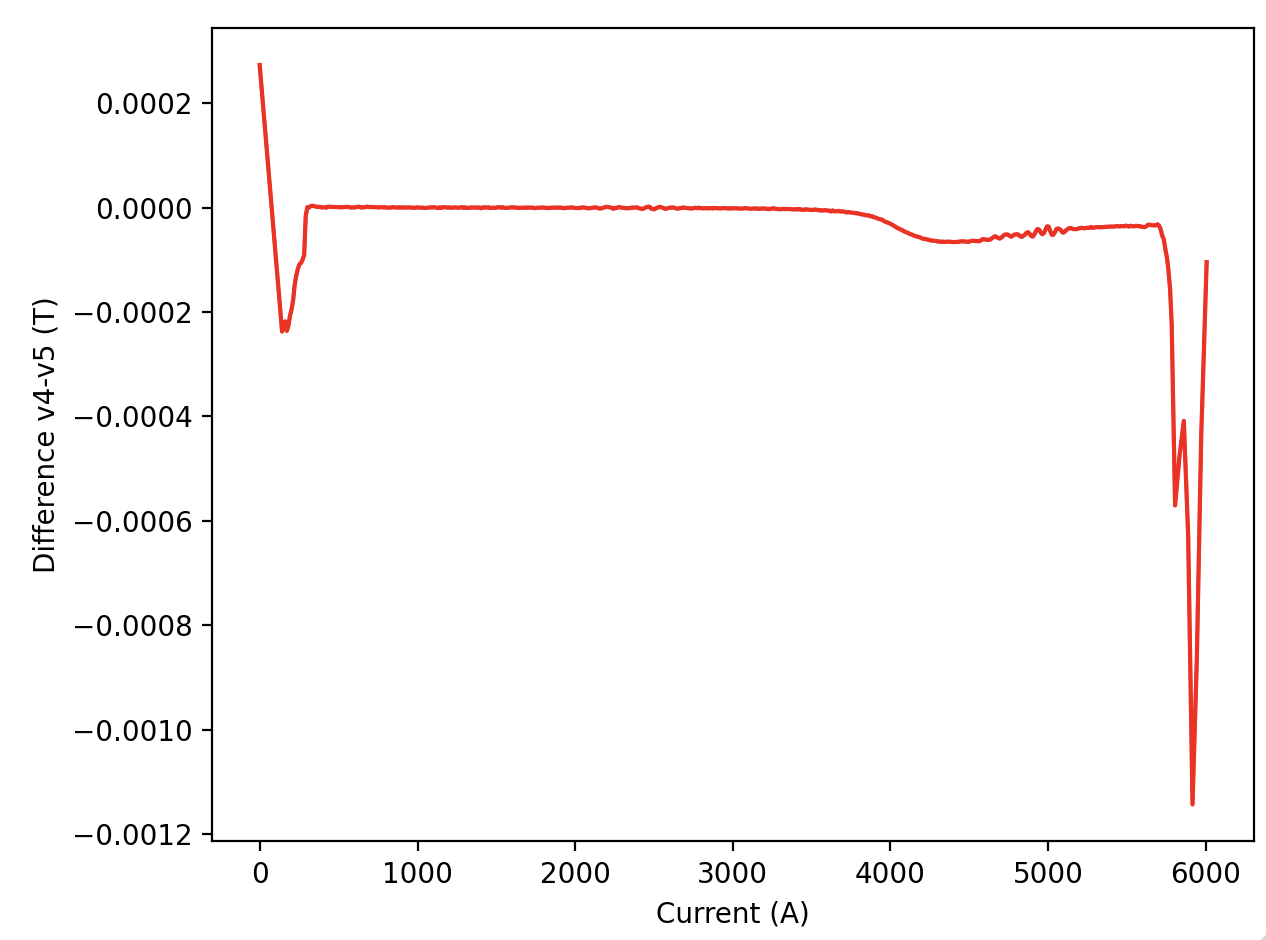
discrete_fn_v5.ys[discrete_fn_v5.xs >= upper_thres] = spline(discrete_fn_v5.xs[discrete_fn_v5.xs >= upper_thres])

The difference between the old and new calibration is shown below. The largest changes can be seen at the lower and upper ends, but also between 4000 and 5000 A there is a lag in the slope because of the savgol filter.

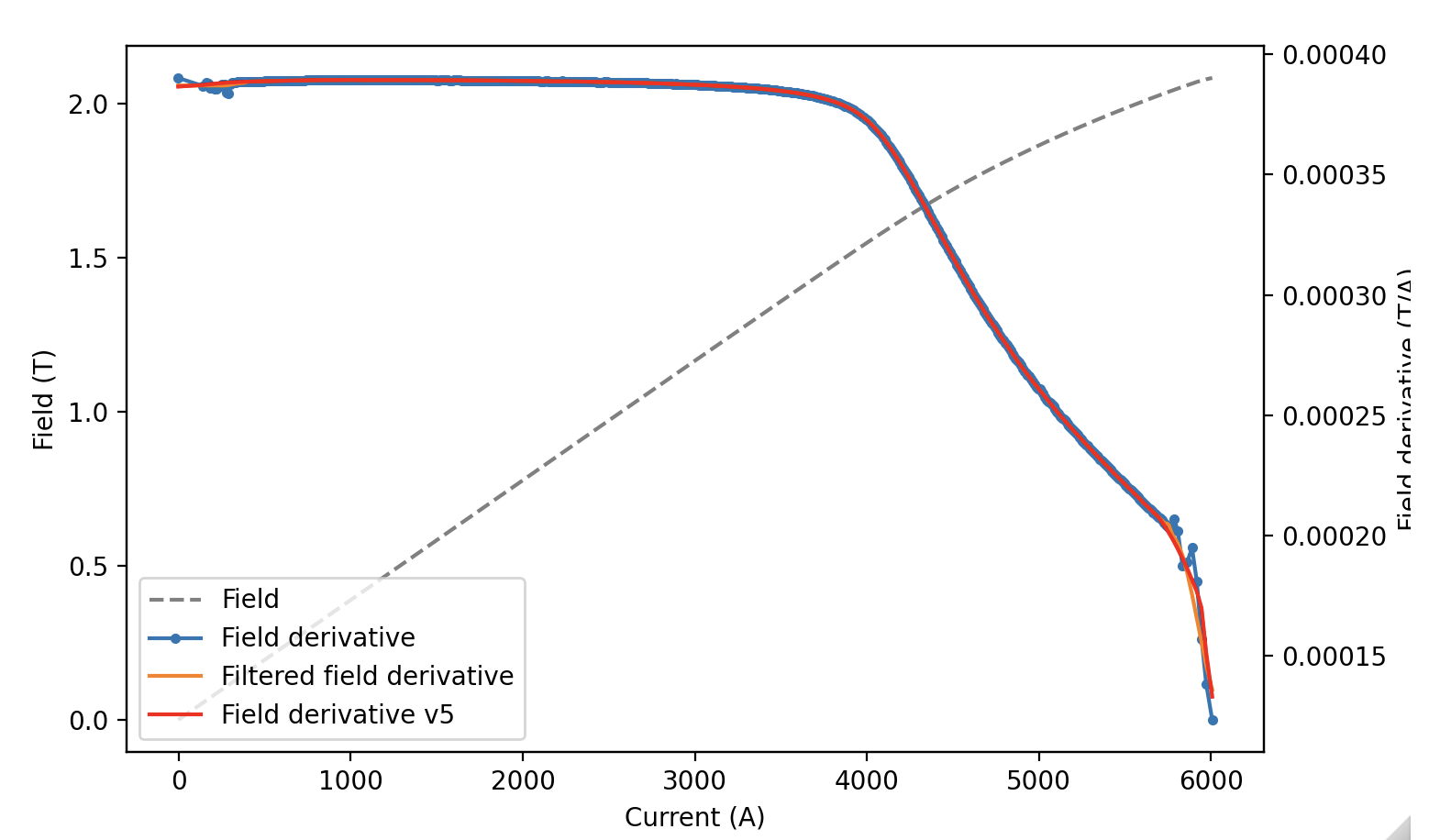
The new fit using a 3rd order univariate spline fits well on the lower end and the upper end, specifically at >5800 A.

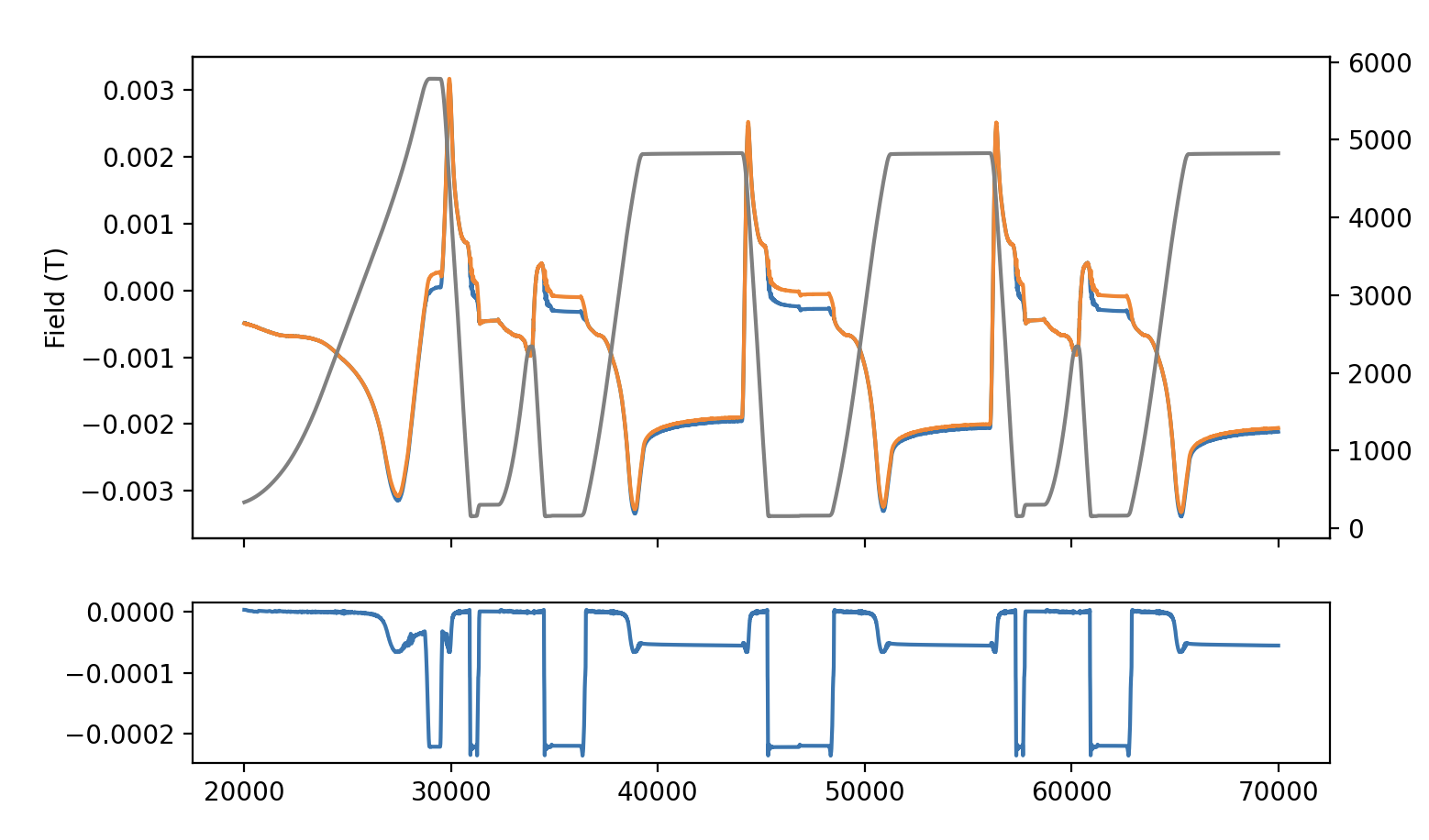
There is a horizontal shift at flat bottom (sub 300 A) and flat top (>5600 A) to to the straightened out calibration function.

The new piecewise linear functions are written to